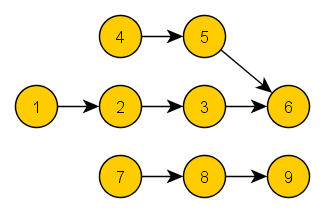
Topological ordering (topological sorting) of a graph is a sequence of its vertices, in which for each edge of the graph holds that
precedes
. Hence only acyclic graph can be ordered topologically.
When a topologically ordered graph is plotted, than all of its edges are oriented exactly in one direction.
Usage of topological ordering
Topological ordering can be, for example, used for planning of mutually dependent events/activities. If we perform activities in their topological order, then each activity will be performed after all activities it is dependent on.
Algorithm
The algorithm for topological ordering is based on depth first search. More specifically it is the order of closing vertices in a inversely oriented graph. The asymptotic complexity of this procedure is , where
is number of vertices of the graph and
is number of its edges.
Code
/**
* Prints out topological ordering of the graph given
* @param graph graph
*/
public static void orderTopologically(GraphIface graph) {
//states of particular nodes
List<Integer> roots = new ArrayList<Integer>();
for (int i = 0; i < graph.getVertexCount(); i++) {
//if it does not have any descendants in original graph
//than it is a root in the inverse graph
if(graph.getEdges(i).size() == 0) roots.add(i);
}
GraphIface inverted = graph.inverse(); //create inversly oriented graph
int[] state = new int[inverted.getVertexCount()];
for (int i = 0; i < state.length; i++) state[i] = FRESH;
for (Integer i : roots) {
doOrdering(inverted, i, state);
}
}
/**
* Perform the topological ordering (sorting)
* @param graph graph
* @param vertexNr number of the current node
* @param state array of states
*/
private static void doOrdering(GraphIface graph, int vertexNr, int[] state) {
state[vertexNr] = OPENED;
for (Integer i : graph.getEdges(vertexNr)) {
if (state[i] == FRESH) doOrdering(graph, i, state);
else if (state[i] == OPENED) throw new IllegalArgumentException("Graph contains cycles");
}
System.out.print(" -> " + vertexNr);
state[vertexNr] = CLOSED;
}
Sources
- KOLÁŘ, Josef. Teoretická informatika. 2. ed. Praha : Česká informatická společnost, 2004. 205 p. ISBN 80-900853-8-5.