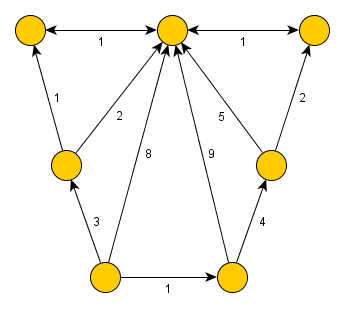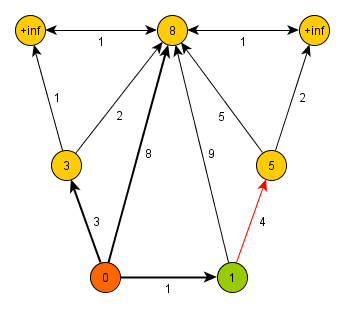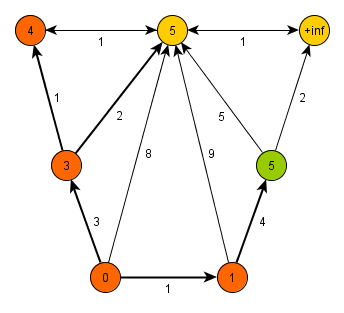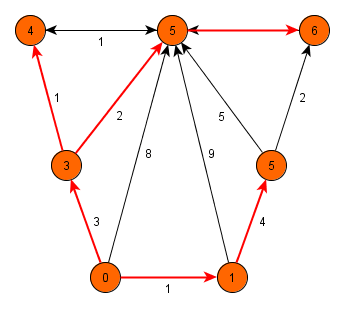
Dijkstra's algorithm is the fastest known algorithm for finding all shortest paths from one node to all other nodes of a graph, which does not contain edges of a negative length. The algorithm was invented by dutch computer scientist Edsger Dijkstra in 1959.
Description
Dijkstra's algorithm can be described as a generalized form of breadth-first search, in which the order of traversed nodes is not determined by number of edges from the root, but as a distance from the root (sum of weights of all edges along the path from root to the given node). As a consequence Dijkstra's algorithm process only those node, for which the shortest path was already discovered.
The algorithm stores all nodes in a priority queue ordered by distance of the node from the root – in the first iteration of the algorithm, only root has distance set to 0, distance of all other nodes is equal to infinity. Than in each step Dijkstra's algorithm picks from the queue a node with the highest priority (least distance from the root) a processes it and reevaluates distances of all unprocessed descendants of the node. This means that the algorithm checks for all descendants that the following condition holds:
If it does hold, the algorithm changes accordingly the distance of the descendant and sets the processed node as his ancestor. When all descendants are checked, the algorithm picks again the node with the highest priority and repeats the procedure.
Dijkstra's algorithm terminates, when the queue is empty (all nodes are processed).
It is important to know that Dijkstra's algorithm requires that weights of all edges are non-negative. Otherwise the procedure is not able to determine whether the shortest path for the node was already found or not.
Complexity
The asymptotic complexity of Dijkstra's algorithm depends on the implementation of the priority queue. If it is implemented using sequential search than the complexity is , where
is number of nodes of the graph. When binary heap is used, the complexity is
(
denotes number of edges).
Code
/**
* Dijkstra's algorithm
* @param d matrix of legths, position [0 1] = 2 means that from node 0 leads an edge to node 1 of length 2
* @param from root node
* @return tree an ancestors (denotes path from the node to the root node)
*/
procedure int[] doDijkstra(d, from) {
//insert all nodes to the priority queue, node from has a distance 0, all others infinity
Q = InsertAllNodesToTheQueue(d, from)
CLOSED = {} //closed nodes - empty set
predecessors = new array[d.nodeCount] //array of ancestors
while !Q.isEmpty() do
node = Q.extractMin()
CLOSED.add(node) //close the node
//contract distances
for a in Adj(node) do //for all descendants
if !CLOSED.contains(a) //if the descendatn was not closed yet
//and his distance has decreased
if Q[node].distance + d[node][a] < Q[a].distance
//zmen prioritu (vzdalenost) uzlu
Q[a].distance = Q[node].distance + d[node][a]
//change its ancestor
predecessors[a] = node
return predecessors
/**
* Dijkstra's algorithm
* @param d matrix of lengths (Integer.MAX_VALUE if there is no edge between the nodes)
* @param from root node
* @return tree an ancestors (denotes path from the node to the root node)
*/
public static int[] doDijkstra(int[][] d, int from) {
Set<Integer> set = new HashSet<Integer>();
set.add(from);
boolean[] closed = new boolean[d.length];
int[] distances = new int[d.length];
for (int i = 0; i < d.length; i++) {
if (i != from) {
distances[i] = Integer.MAX_VALUE;
} else {
distances[i] = 0;
}
}
int[] predecessors = new int[d.length];
predecessors[from] = -1;
while (!set.isEmpty()) {
//find the nearest node
int minDistance = Integer.MAX_VALUE;
int node = -1;
for(Integer i : set){
if(distances[i] < minDistance){
minDistance = distances[i];
node = i;
}
}
set.remove(node);
closed[node] = true;
//contract the distances
for (int i = 0; i < d.length; i++) {
//edge exists
if (d[node][i] != Integer.MAX_VALUE) {
if (!closed[i]) {
//the path length decreased using the ancestor node
if (distances[node] + d[node][i] < distances[i]) {
distances[i] = distances[node] + d[node][i];
predecessors[i] = node;
set.add(i);
}
}
}
}
}
return predecessors;
}
Sources
- KOLÁŘ, Josef. Teoretická informatika. 2. ed. Praha : Česká informatická společnost, 2004. 205 p. ISBN 80-900853-8-5.